Problem: Determine whether the following series converges.
![]()
Problem: Determine whether the following series converges.
![]()
Problem: Determine whether the following series converges.
![]()
Problem: Determine whether the following series converges.
![]()
Problem: Determine whether the following series converges.
![]()
Problem: Determine whether the following series converges.
![]()
Problem: Determine whether the following series converges.
![]()
Problem: Determine whether the following series converges.
![]()
Problem: Determine whether the following series converge.
![]()
Problem: Determine whether the following series converges absolutely.
![]()
Problem: Determine whether the following series converges absolutely.
![]()
Problem: Investigate convergence of the following series. (Does it converge? If it does, then how?)
![]()
Problem: Investigate convergence of the following series. (Does it converge? If it does, then how?)
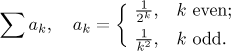
Problem: Investigate convergence of the following series. (Does it converge? If it does, then how?)
![]()
Problem: Investigate convergence of the following series. (Does it converge? If it does, then how?)
![]()